Linear regression

This page is a part of PSPP Guide.

Linear regression refers to any approach to modelling the relationship between dependent variable and one or more independent variables, such that the model depends linearly on the unknown parameters to be estimated from the data. Such a model is called a “linear model”. Linear regression procedure in PSPP fits linear models to data via least-squares estimation. The procedure is appropriate for data which satisfy assumptions typical in linear regression.

In our example we will use variables from SJM 2002/2 data set. TV, radio and news (newspapers; don’t know” answers are recoded to system missing) are independent variables, and happy (”don’t know” answers also recoded to system missing) is dependent variable.

To do regression analysis go to Analyze – Linear Regression.

You can also set to save predicted values and residuals as a new variables (by clicking to Save button).

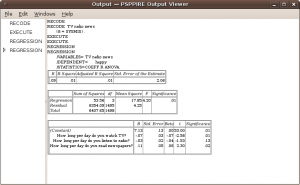
The results show that linear model is OK (F-test is statistically significant), however only 1% of the total variance (of variable happy) is explained (by TV, radio and news).

The model shows that only TV and news has statistically significant influence on happy, TV has small negative influence (correlation coefficient beta is -0.7) and news has small positive influence (correlation coefficient beta is -0.6). Analysis show that people who watch TV more time per day are a little more unhappy and people who read newspaper more time per day are a little more happy.